Figures:

Click here to read the full report.
Abstract:
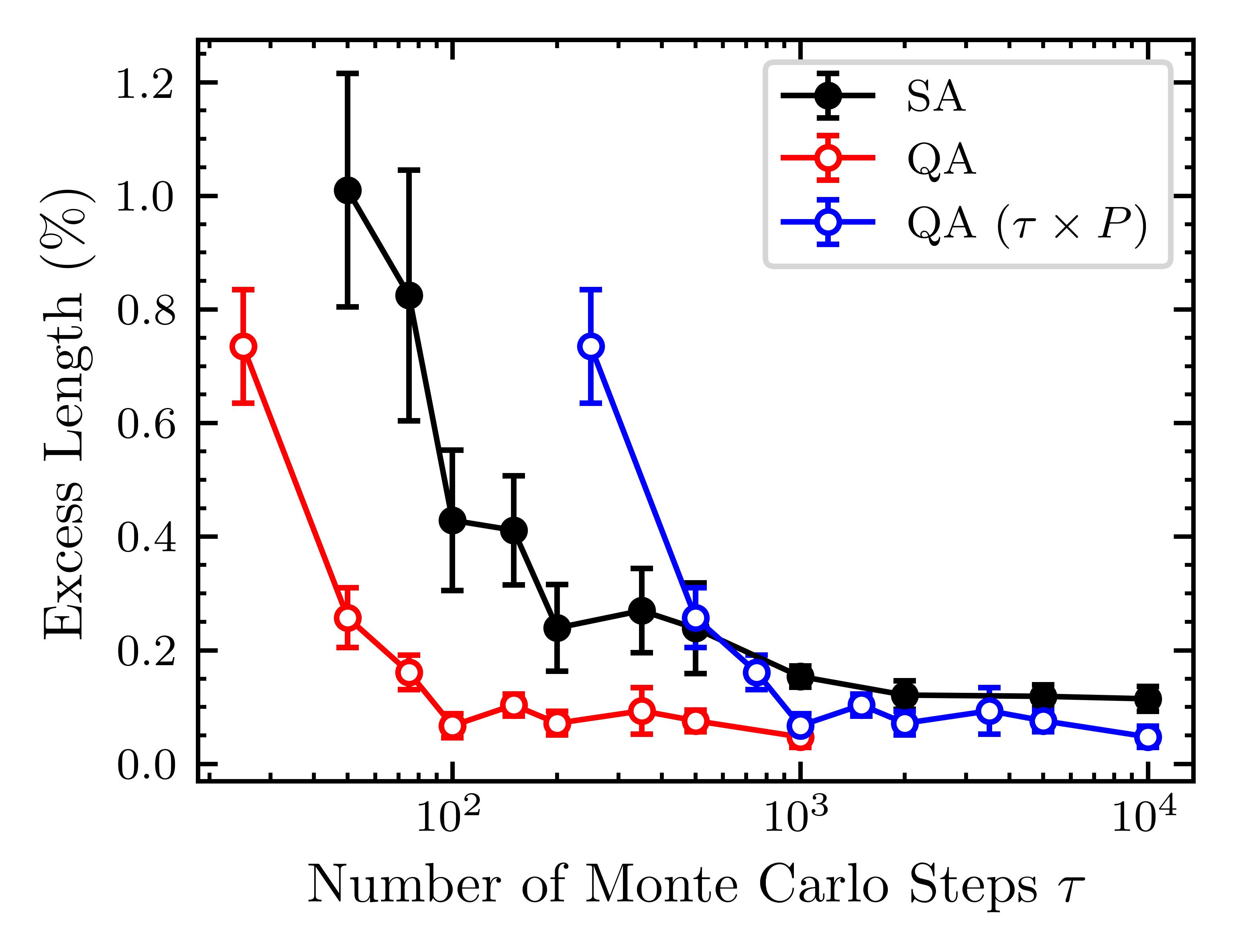
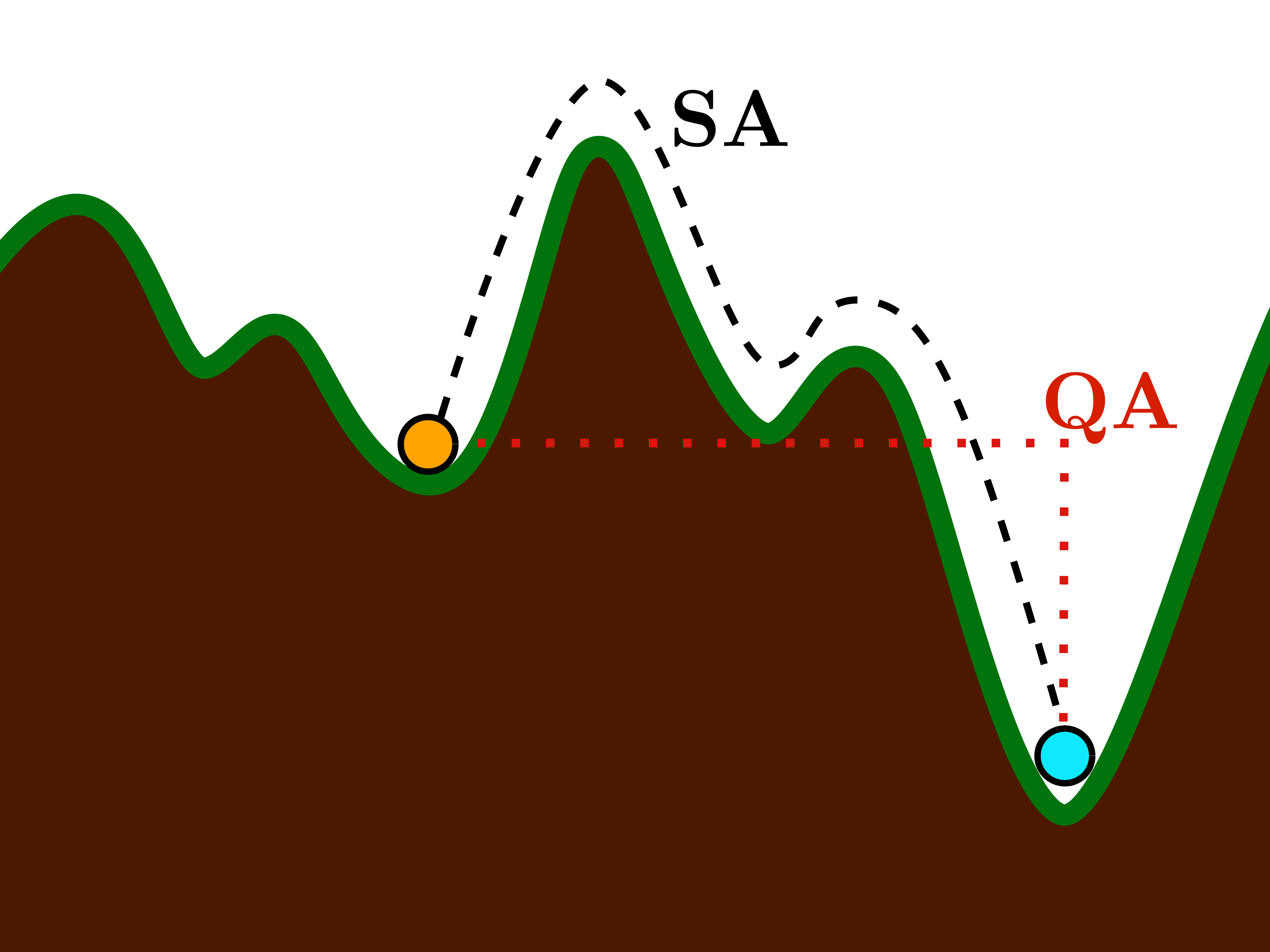
Solving combinatorial optimisation (CO) problems efficiently is an important challenge that spans various domains. In this report, we investigate and compare two prominent meta-heuristic approaches to tackle CO problems: simulated annealing (SA) and quantum annealing (QA). We use a 16-city instance of the Travelling Salesman Problem (TSP) as a test example and solve it via standard Monte Carlo SA and path-integral Monte Carlo (PIMC) QA. We determine the range of initial temperature T0 for SA, as well as the ranges of Trotter number P and ambient temperature T for QA, that yield the most efficient and accurate results through studies of the dependence of the final residual length on each method’s parameters. The superiority of PIMC QA relative to SA is demonstrated, for this TSP, with a study of the dependence of the final residual length on the total number of Monte Carlo steps. These results suggest QA could be an even better general-purpose CO meta-heuristic than SA. Future areas of investigation for QA and quantum optimisation as a whole are suggested.

Python code is available at GitHub

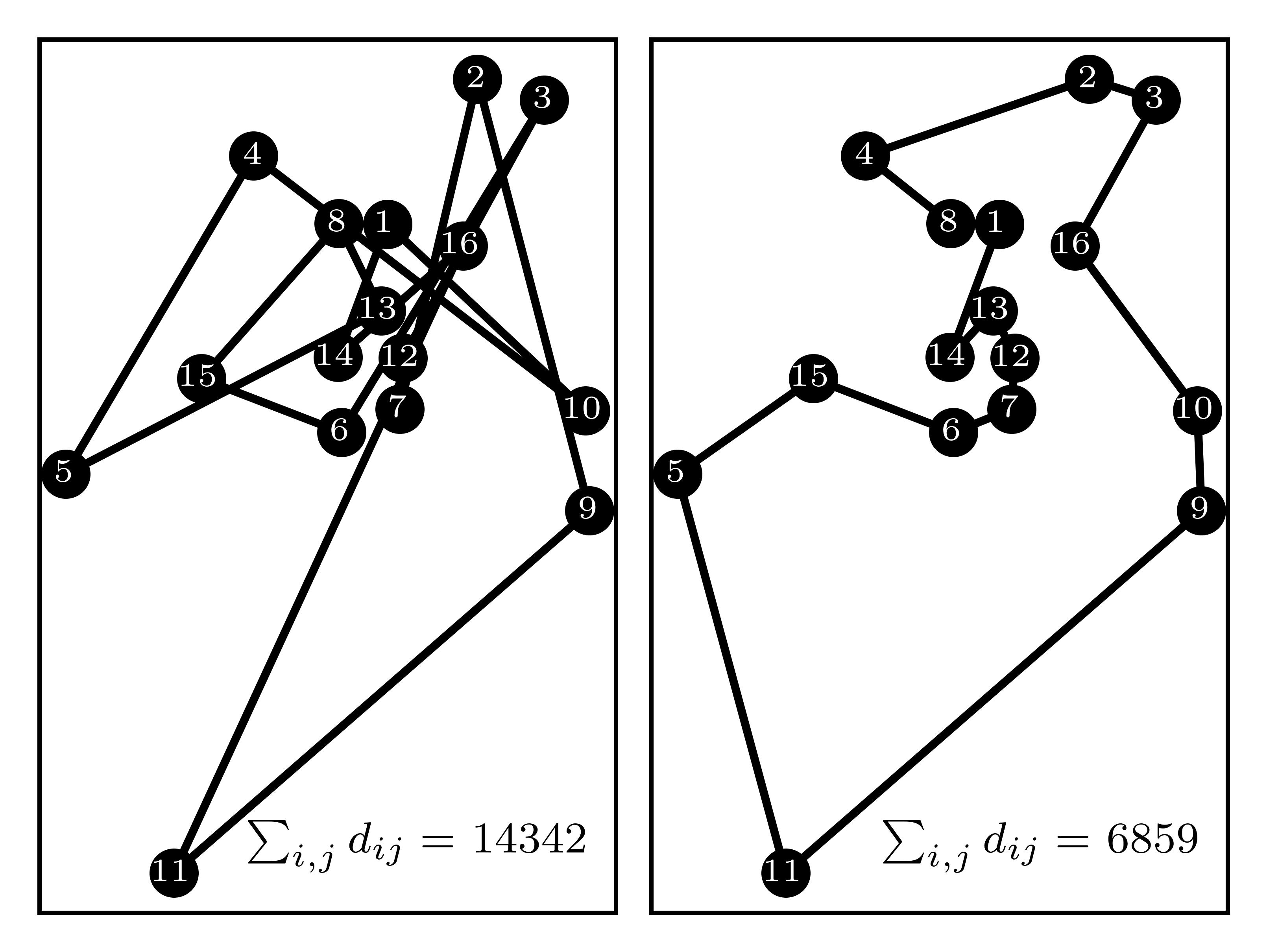
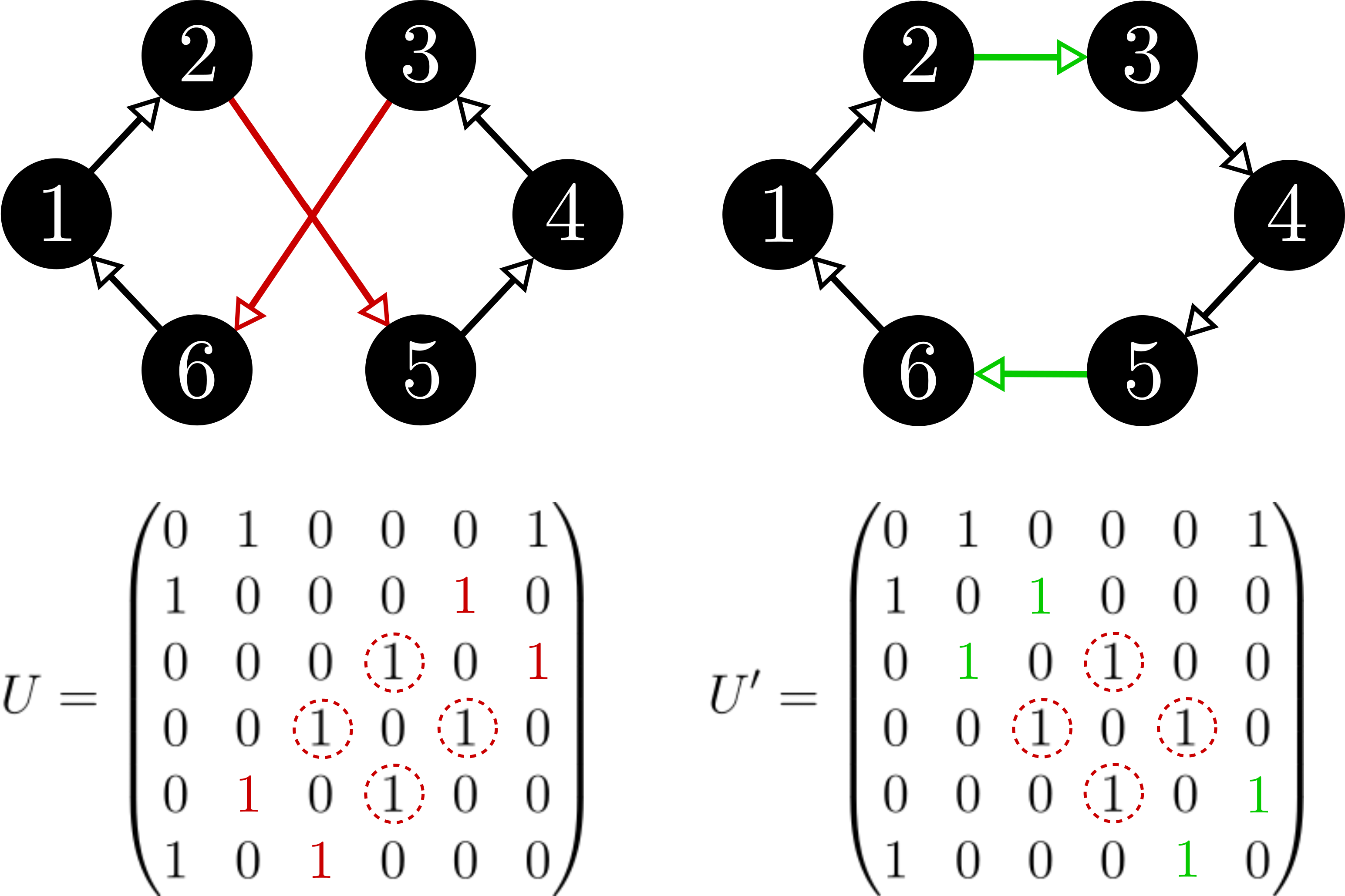
Combinatorial optimisation is the act of finding the ideal combination of a set of objects subject to a set of constraints, its applications span biology, engineering, computer science, and applied mathematics. In this work, we solve a simple instance of the combinatorial optimisation problem Maximal Independence Set, see Fig. 1, with Adiabatic Quantum Computing simulated via numerical integration of the Schrödinger equation, and suggest that a running time of 18s is optimal, giving an acceptable success probability of 0.99, see Fig. 2.
Whilst this numerical integration technique is effective for small problems, the memory it requires scales exponentially with problem size. In the project above, I investigate quantum Monte Carlo, a more efficient simulation techique based on similar physical principles.

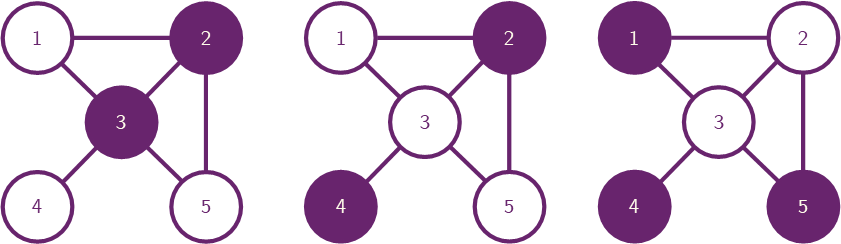
Fig. 1: The instance of Maximal Independent Set we investigated. From left to right: a set which isn’t independent, a set which is independent but not the maximum, the maximal independent set.

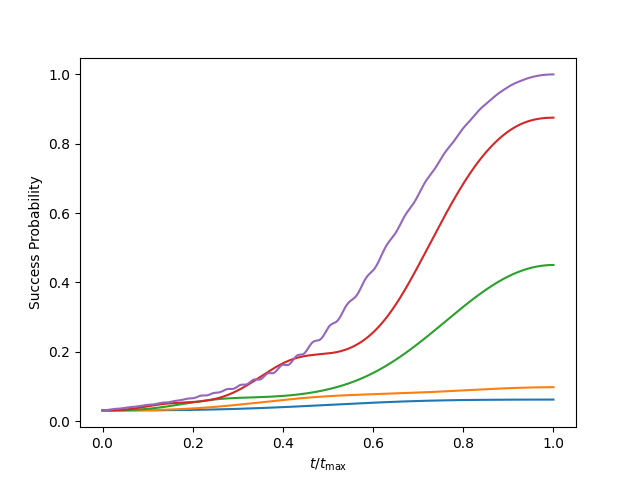
Fig. 2: Success probability against time for tmax of 1 (blue), 2 (orange), 5 (green), 10 (red), 100 (purple).

Fig. 3: Instantaneous probability of measuring the system in each state over the course of the annealing.

Python code is available at GitHub

Fig. 1: A ring under diametral compression illuminated by white light. The polarisation of incident and outgoing light is changed by π / 10 radians between each frame, rotating the isoclinic fringes but keeping the isochromatics stationary.

Click here to read the full report.
Abstract:
Understanding how objects behave under stress is crucial in many areas of engineering and materials science, spanning applications from aerospace to bio-engineering. Several numerical methods of stress analysis for complex structures exist, but they are computationally intensive and, therefore, expensive to run. A cheaper, quicker and simpler alternative to such methods is therefore required. Such an alternative is the experimentally-based process of digital photoelasticity. In this report, two methods of digital photoelasticity are investigated: the analytical ten-step phase-shifting technique based on Jones calculus (Ramji and Ramesh, 2008), and StressUnet, a convolutional neural network based on the U-Net architecture (Zhao et al., 2022). The simplicity and low time requirement of stress analysis with StressUnet compared to stress analysis with the phase-shifting technique are highlighted. Both methods are shown to perform inconsistently when evaluated on experimentally obtained data, but StressUnet is shown to perform robustly when evaluated on a large, diverse set of computer-generated data. Experimental setup improvements for both methods are proposed, implementing the adaptive quality guided phase unwrapping algorithm (Ramji, 2010) and increasing the number of training epochs are suggested as improvements to the phase-shifting technique and StressUnet, respectively. Read more ...

Applying Deep Learning to automate classification of shape features in low-grade gliomas.
Aiming to reproduce the results of Buda et al.
Project is described in more detail on GitHub

Implementations, from scratch with NumPy, of Gaussian, Median and Bilateral noise removal filters.
Project is described in more depth on GitHub

Music generated in real time by a recurrent neural network trained on scraped MIDI tracks.
The project was completed in 24 hours, reaching the semi-final of DurHack 2023.
See more on GitHub

Click here to read the full report.
Abstract:
The search for dark matter has been a central focus in astrophysics since the term was first coined by Zwicky in 1933. This report builds on the pioneering work of Rubin et al. (1980), employing a multi-faceted approach to investigate the dark matter content of the spiral galaxy M82. Through analysis of its rotation curve from HI and CO emission lines, as well as luminosity calculations via CCD photometry in the V-band, we determine the mass-to-light ratio of M82 to be 0.6 ± 0.8 Υ_⊙, an order of magnitude lower than that of Andromeda, and demonstrate that the rotation curve is Keplerian, consistent with that of a galaxy with mass concentrated in the central bulge. We conclude that M82 lacks an extended dark matter halo, challenging prevailing theories of dark matter distributions in spiral galaxies.

Fig. 1: Stacked BVR image of M82 taken from Durham on 06/02/2020, each image had an exposure time of 30s. An ellipse is overlaid to demonstrate the type of aperture used to extract luminosity data, R is the semi-major axis.

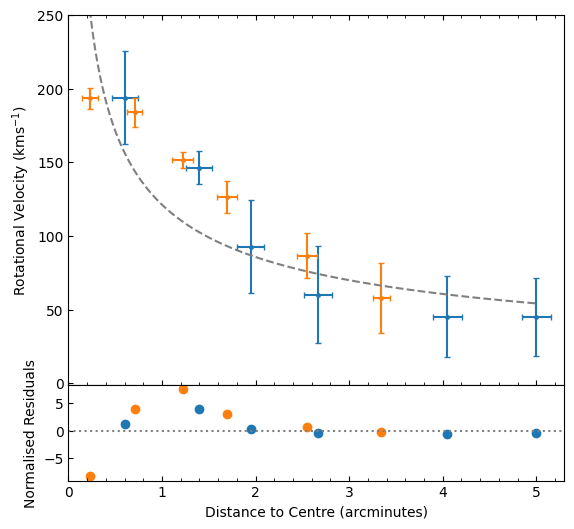
Fig. 2: Rotation curve for M82 obtained from Doppler-shift of HI lines (blue) and CO-lines (orange) as measured by Sofue et al. in 1992 and Yun et al. in 1993 respectively. Rotation curve for a point mass (dashed) is indicated, normalised residuals are plotted below.